Merkling on Ethereum | Ethereum Foundation Blog

Merkle trees are the fundamental elements that make blockchains work. While it is certainly possible in theory to create a blockchain without a Merkle tree, simply creating a huge block header containing all transactions directly makes the ability to use the blockchain trustless out of reach of most people. This creates major scalability issues. A powerful computer for the long term. Thanks to Merkle trees, it is possible to build an Ethereum node that runs on any computer, large or small, laptop, smartphone, or even Internet of Things devices. Slock.it. So how exactly do these Merkle trees work and what value do they provide now and in the future?

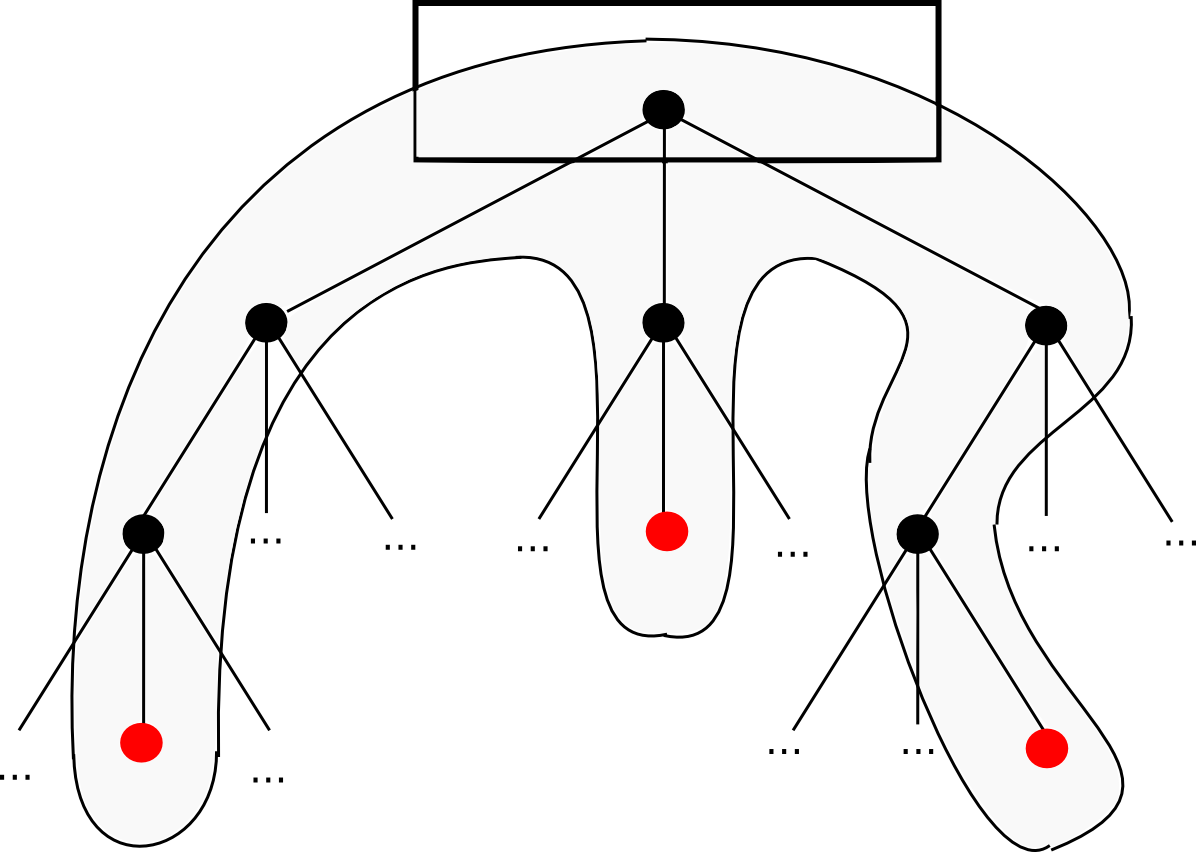
First, the basics. In the most general sense, a Merkle tree is a method of hashing together large numbers of “chunks” of data, relying on partitioning the chunks into buckets. Each bucket contains only a few chunks and then we get the hash of each bucket. Repeat the same process until the total number of hashes remaining becomes the root hash.

The most common and simplest form of Merkle tree is the binary Mekle tree. Here, a bucket always consists of two adjacent chunks or hashes. It can be described as follows:

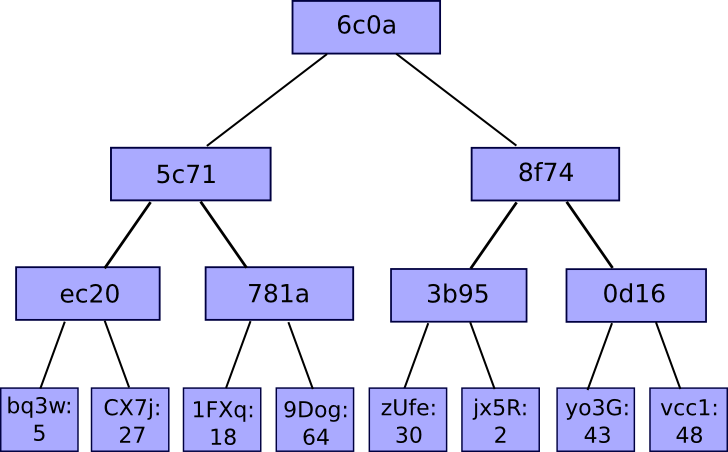
So what are the benefits of this strange kind of hashing algorithm? What if we concatenate all the chunks into one big chunk and use a regular hashing algorithm on it? The answer is that it allows for a neat mechanism known as a Merkle proof.

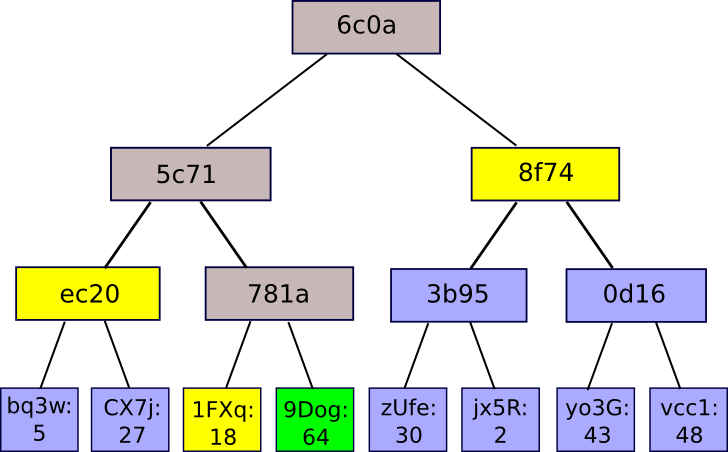
A Merkle proof consists of a chunk, the root hash of the tree, and a “branch” consisting of all the hashes going up the path from the chunk to the root. Anyone reading the proof can see that the hashing for at least that branch progresses consistently up the tree, so that a given chunk is actually at that location in the tree. The application is simple. Suppose you have a large database, and the entire contents of the database are stored in a Merkle tree where the root of the Merkle tree is publicly known and trusted (i.e., it has been digitally signed by a sufficiently trusted party). , or there is a lot of evidence for the work). Then, a user who wants to perform a key-value lookup in the database (e.g. “Please tell me the object at position 85273”) can request a Merkle proof, and when received, verifies that it is correct. value received Actually That specific root is located at location 85273 in the database. Allows for authentication mechanisms. small Amount of data, such as a hash, to scale for authentication. large in size A database of potentially unlimited size.

Bitcoin’s Merkle Proof

The original application of Merkle proof was in Bitcoin, described and created by Satoshi Nakamoto in 2009. The Bitcoin blockchain uses Merkle proofs to store transactions in every block.

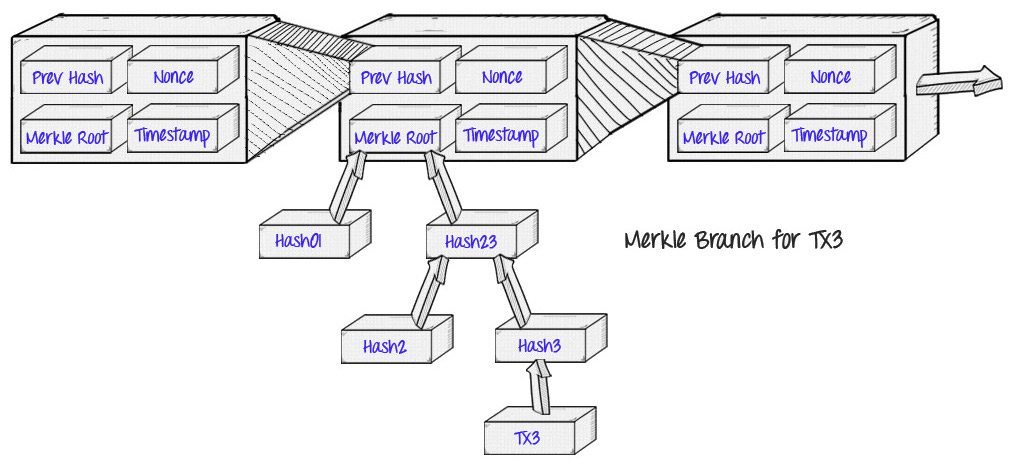
The benefit this provides is a concept that Satoshi describes as “simplified payment verification” instead of downloading. every Transactions and all blocks, “light clients” can only download the chain. block header80-byte data chunks for each block containing only 5 items:

• Hash of previous header
• timestamp
• Mining Difficulty Value
• temporary proof of work
• The root hash of the Merkle tree containing the transactions for that block.

When a light client wants to verify the status of a transaction, it can request a Merkle proof showing that the root of a particular transaction is in one of the Merkle trees in the block header of the main chain.

This helps us a lot, but it has its limitations as a Bitcoin-style light client. One particular limitation is that while you can prove the inclusion of a transaction, you cannot prove anything about its current state (e.g. holding a digital asset, registering its name, state of a financial contract, etc.). How many Bitcoins do you have now? Bitcoin Lite clients can use a protocol that queries multiple nodes and trusts that at least one of them will tell you about a specific transaction spend from your address, which can go quite far for that use case, but could be used for other more complex applications. This will help you. Not nearly enough. The exact nature of a transaction’s effects may depend on the effects of multiple previous transactions, which in turn depend on the previous transaction, so ultimately every single transaction across the entire chain must be authenticated. To solve this problem, Ethereum takes the Merkle tree concept one step further.

Ethereum’s Merkle Proof

Every block header in Ethereum contains not just one Merkle tree. three Trees for three kinds of objects:

• work
• Receipt (basically a piece of data showing: effect of each transaction)
• situation

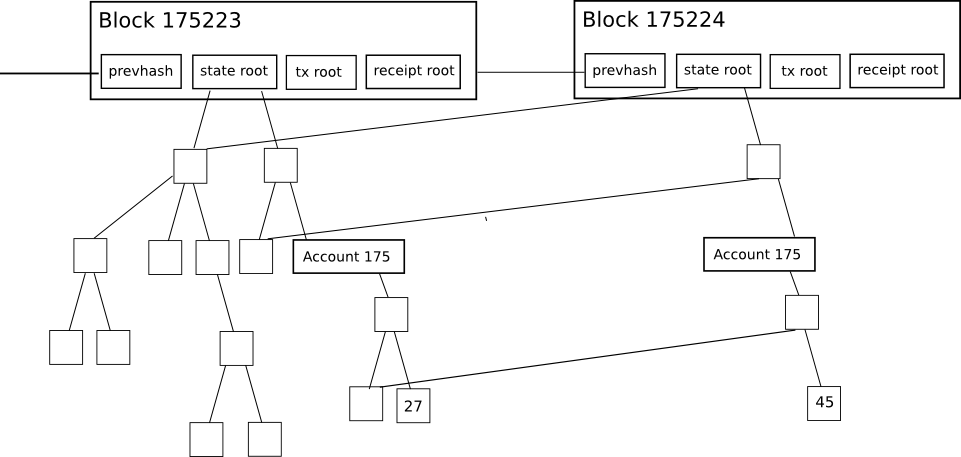
This enables an advanced light client protocol that allows light clients to easily create and obtain verifiable answers to many kinds of queries.

• Is this transaction included in a specific block?
• Please tell us all instances of type
• What is the current balance on my account?
• Does this account exist?
• Pretend to execute this transaction in this contract. What will be the result?

The first is handled by the transaction tree. The third and fourth are handled by the state tree and the second by the receive tree. The first four are very simple to calculate. The server simply finds the object, gets a Merkle branch (a list of hashes going up from the object to the root of the tree), and then responds to the light client with that branch.

The fifth is also handled by the state tree, but the calculation is more complex. Here we Merkle state transition proof. Essentially, it is proof of your claim “if you execute the trade”. tea With root SThe result will be a root state. S’Includes logs L and output o” (The concept of “output” exists in Ethereum because every transaction is a function call. In theory, it is not needed.)

To compute the proof, the server creates a fake block locally, sets its state to S, and pretends to be a light client while applying the transaction. That is, when applying a transaction requires the client to check the balance of an account, the light client performs a balance query. If a light client needs to check for a specific item in a specific contract store, the light client will make a query for it, and so on. The server “answers” all of its own queries correctly, but keeps track of all the data it sends back. The server then sends the combined data of all these requests to the client as evidence. The client then performs exactly the same procedure, but Use the provided evidence as a database; If the result is the same as claimed by the server, the client accepts the proof.

patricia wood

We mentioned above that the simplest kind of Merkle tree is a binary Merkle tree. However, the trees used in Ethereum are more complex. This is the “Merkle Patricia tree” you can hear in the documentation. This article does not cover detailed specifications. that’s the best way this article and this oneLet’s discuss the basic reasoning.

A binary Merkle tree is a very useful data structure for authenticating information in the form of a “list”. Essentially, it’s a series of chunks listed one after another. This is also good for transaction trees because it doesn’t matter how long it takes. edit Wood is like a solid that once created is frozen forever.

However, for state trees, the situation is more complicated. The state of Ethereum essentially consists of a key-value map. Here, the keys are addresses and the values ​​are account declarations, listing each account’s balance, nonce, code, and repository (the repository itself is a tree). For example, the Morden testnet creation status is:

    "0000000000000000000000000000000000000001": 
        "balance": "1"
    ,
    "0000000000000000000000000000000000000002": 
        "balance": "1"
    ,
    "0000000000000000000000000000000000000003": 
        "balance": "1"
    ,
    "0000000000000000000000000000000000000004": 
        "balance": "1"
    ,
    "102e61f5d8f9bc71d0ad4a084df4e65e05ce0e1c": 
        "balance": "1606938044258990275541962092341162602522202993782792835301376"
    

However, unlike transaction history, the status must be updated frequently. Balances and nonce values ​​of accounts change frequently, moreover new accounts are frequently inserted, and keys in the store are frequently inserted and deleted. So what we want is a data structure that allows us to quickly calculate a new tree root after an insert, update edit or delete operation without having to recompute the entire tree. There are also two secondary characteristics that are very desirable.

• Even if an attacker were to intentionally create transactions to make the tree as deep as possible, there is a limit to the depth of the tree. Otherwise, an attacker could perform a denial-of-service attack by manipulating the tree so deeply that each individual update becomes extremely slow.
• The root of the tree depends only on the data, not the update order. Even if you update in a different order and recalculate the tree from scratch, the root should not change.

that much patricia wood, in short, is probably the closest way to achieve all these properties simultaneously. The simplest explanation of how it works is that the key where the value is stored is encoded into a “path” that must be taken down the tree. Since each node has 16 children, the path is determined by hexadecimal encoding. For example key dog encoded in hexadecimal 6 4 6 15 6 7, so you start at the root, go down to the sixth child, fourth child, and so on, until you reach the end. In practice, there are some additional optimizations that can be done to make the process much more efficient when the tree is sparse, but this is the basic principle. two article talking on All features are explained in much more detail.