Advanced Contract Programming Example: SchellingCoin

Writing effective decentralized applications in Ethereum is at the same time easy and hard. The easy part we all know: rather than needing to create your own blockchain, manage complicated database code, deal with networking and NAT traversal, or any of the other complexities involving writing a peer-to-peer app from scratch, you can write code in a simple, high-level programming language like Serpent or Mutan (or LLL if you prefer mucking around a bit lower-level), with the simplicity of a toy scripting language but the power and security of a full blockchain backing it up. An entire implementation of a basic name registry can be done in two lines of code that encompass the essential logic of the program: if not contract.storage(msg.data(0)): contract.storage(msg.data(0)) = msg.data(1). Use the zeroth data item in the message as a key and the first as a value; if the key is not yet taken then set the key to the desired value. A phone book that you can add entries to, but where entries, once made, cannot be changed. However, there is also a hard part: decentralized applications are likely to involve logic that is fundamentally complex, and there is no way that any simplifications to the programming environment can ever remove that fact (however, libraries built on top of the programming language might alleviate specific issues). Furthermore, any dapps doing anything truly interesting is likely to involve cryptographic protocols and economics, and we all know how complex those are.
The purpose of this article will be to go through a contract that is an important component of a fully decentralized cryptoeconomic ecosystem: a decentralized oracle. The oracle will be implemented using the SchellingCoin protocol, described in a previous blog post. The core idea behind the protocol is that everyone “votes” on a particular value (in this case, we’ll use wei per US cent as an example, as that will end up very useful in financial contracts), and everyone who submitted a vote that is between the 25th and 75 percentile (ie. close to median) receives a reward. The median is taken to be the “true value”. In order to increase security, each round is done via a two-step commitment protocol: in the first phase, everyone selects a value P which is the value they will be voting for, and submits H = sha3((msg.sender, P)) to the contract, and in the second phase everyone submits the P that they selected and the contract accepts only those values that match the previously provided hash. Rewarding and evaluation is then done at the end.
The reason why it works is this. During the first phase, everyone is so to speak “in the dark”; they do not know what the others will be submitting, seeing perhaps only hashes of other votes. The only information they have is that they are supposed to be submitting the price of a US cent in wei. Thus, knowing only that the only value that other people’s answers are going to be biased towards is the actual wei/UScent, the rational choice to vote for in order to maximize one’s chance of being near-median is the wei/UScent itself. Hence, it’s in everyone’s best interests to come together and all provide their best estimate of the wei/UScent price. An interesting philosophical point is that this is also the same way that proof-of-work blockchains work, except that in that case what you are voting on is the time order of transactions instead of some particular numeric value; this moderately strongly suggests that this protocol is likely to be viable at least for some applications.
Of course, in reality various kinds of special scenarios and attacks are possible, and the fact that the price of any asset is quite often controlled by a small number of centralized exchanges makes things more difficult. For example, one imaginable failure mode is that if there is a market share split between the BTC/USD on Bitstamp, Bitfinex and MtGox, and MtGox is the most popular exchange, then the incentives might drive all the votes to aggregate around the GOX-BTC/USD price specifically, and at that point it is entirely unclear what would happen when MtGox gets hacked and the price on that exchange alone, and not the others, falls to $100. Everyone may well end up following their individual incentives and sticking to each other to the protocol’s collective doom. How to deal with these situations and whether or not they are even significant is an entirely empirical issue; it is hard to say what the real world will do beforehand.
Formalizing the protocol, we have the following:
- Every set of N blocks (here, we set N = 100) constitutes a separate “epoch”. We define the epoch number as floor(block.number / 100), and we define the block number modulo 100 to be the “residual”.
- If the residual is less than 50, then anyone can submit a transaction with any value V and hash H = sha3((msg.sender, R, P)), where P is their estimate of the price of 1 US cent in wei (remember, 1 wei = 10-18 ether, and 1 cent = 10-2 USD) and R is a random number.
- If the residual is greater than 50, then anyone who submitted a hash can submit P, and the contract will check if sha3((msg.sender, P)) matches the hash.
- At the end of the epoch (or, more precisely, at the point of the first “ping” during the next epoch), everyone who submitted a value for P between the 25th and 75th percentile, weighted by deposit, gets their deposit back plus a small reward, everyone else gets their deposit minus a small penalty, and the median value is taken to be the true UScent/wei price. Everyone who failed to submit a valid value for P gets their deposit back minus a small penalty.
Note that there are possible optimizations to the protocol; for example, one might introduce a feature that allows anyone with a particular
Pvalue to steal the deposit from whoever submitted the hash, making it impractical to share one’s
Pto try to influence people’s votes before residual 50 hits and the second phase starts. However, to keep this example from getting too complicated we will not do this; additionally, I personally am skeptical of “forced private data revelation” strategies in general because I predict that many of them will become useless with the eventual advent of generalized zero-knowledge proofs, fully homomorphic encryption and obfuscation. For example, one might imagine an attacker beating such a scheme by supplying a zero-knowledge proof that their
Pvalue is within a particular 1015 wei-wide range, giving enough information to give users a target but not enough to practically locate the exact value of
P. Given these concerns, and given the desire for simplicity, for now the simple two-round protocol with no bells-and-whistles is best.
Before we start coding SchellingCoin itself, there is one other contract that we will need to create: a sorting function. The only way to calculate the median of a list of numbers and determine who is in a particular percentile range is to sort the list, so we will want a generalized function to do that. For added utility, we will make our sorting function generic: we will sort pairs instead of integers. Thus, for examples, (30, 1, 90, 2, 70, 3, 50, 4) would become ( 30, 1, 50, 4, 70, 3, 90, 2 ). Using this function, one can sort a list containing any kind of object simply by making an array of pairs where the first number is the key to sort by and the second number is a pointer to the object in parent memory or storage. Here’s the code:
if msg.datasize == 0: return((), 0) else: low = array(msg.datasize) lsz = 0 high = array(msg.datasize) hsz = 0 i = 2 while i < msg.datasize: if msg.data(i) < msg.data(0): low(lsz) = msg.data(i) low(lsz + 1) = msg.data(i + 1) lsz += 2 else: high(hsz) = msg.data(i) high(hsz + 1) = msg.data(i + 1) hsz += 2 i = i + 2 low = call(contract.address, low, lsz, lsz) high = call(contract.address, high, hsz, hsz) o = array(msg.datasize) i = 0 while i < lsz: o(i) = low(i) i += 1 o(lsz) = msg.data(0) o(lsz + 1) = msg.data(1) j = 0 while j < hsz: o(lsz + 2 + j) = high(j) j += 1 return(o, msg.datasize)
Computer students may recognize this as a quicksort implementation; the idea is that we first split the list into two, with one half containing everything less than the first item and the other half containing everything greater, then we recursively sort the first and second lists (the recursion terminates eventually, since eventually the sub-lists will have zero or one items, in which case we just return those values directly), and finally we concatenate output = sorted_less_than_list + first item + sorted_greater_than_list and return that array. Now, putting that into “quicksort_pairs.se”, let’s build the code for the actual SchellingCoin. Feel free to go to the github to see the code all in one piece; here, we will go through it a few lines at a time.
First, some initialization code:
init: contract.storage(0) = block.number contract.storage(3) = create('quicksort_pairs.se') code: HASHES = 2^160 VALUES = 2^170
The first code block sets contract storage index 0 to the current block number at initialization time, and then creates a quicksort contract and saves that in storage index 3. Note that theoretically you would want to just create the quicksort contract once and refer to it by address; we’re just doing an inline create for simplicity and to show the feature. In the code we start off by declaring two variables to serve as pseudo-constants; HASHES = 2160 as the pointer for where we store hashes, and VALUES = 2170 as the pointer for where we store values from the second phase.
Now, from here let’s skip to the bottom half of the code, because that turns out to be more convenient and it’s the code that actually gets run “first” over the course of the contract’s lifetime.
# Hash submission if msg.data(0) == 1: if block.number % 100 < 50: cur = contract.storage(1) pos = HASHES + cur * 3 contract.storage(pos) = msg.data(1) contract.storage(pos + 1) = msg.value contract.storage(pos + 2) = msg.sender contract.storage(1) = cur + 1 return(cur) # Value submission elif msg.data(0) == 2: if sha3((msg.sender, msg.data(3), msg.data(2)), 2) == contract.storage(HASHES + msg.data(1) * 3): contract.storage(VALUES + msg.data(1)) = msg.data(2) return(1) # Balance request elif msg.data(0) == 3: return(contract.balance) # Value request else: return(contract.storage(2))
The first important paradigm that we see here is using msg.data(0) to refer to a “message type”; messages with zeroth data item 1 are hash submissions, 2 are value submissions, 3 are balance requests and 4 are requests for the current UScent/wei price. This is a standard interface that you will likely see across very many contracts. The first clause, the one for submitting hashes, is somewhat involved, so let us break it down step by step. The primary purpose here is to allow people to submit hashes, and record submissions in storage. To that end, the contract is storing the data sequentially in storage starting at index 2160. We need to store three pieces of data – the actual hash, the size of the accompanying deposit, and the sender address, for each hash, so we do that. We also use storage index 1 to store how many hashes have already been submitted. Thus, if two hashes have been submitted, storage will look something like this:

The precise instructions in the clause are:
- Proceed only if the residual is less than 50.
- Set the variable cur to storage index 1, where we are going to be storing the number of hashes that have already been submitted
- Set the variable pos to the index in storage in which we will be putting the new hash
- Save the hash (supplied as the first data item), the sender address and the value in storage
- Set the new number of hashes to cur + 1
- Return the index of the hash supplied
Technically, if the only users of SchellingCoin are people, step 5 is unnecessary; although the index will be necessary in a later step, a smart client could potentially simply scan the
cur variable immediately after the transaction, removing the need for the opcodes needed to handle the return. However, since we expect that in Ethereum we will have plenty of instances of contracts using other contracts, we will provide the return value as a habit of good machine interface.
The next clause is for submitting values. Here, we ask for two data items as input: the index where the hash was saved during the first step of the protocol (this is the return value of the previous clause), and the actual value. We then hash the sender and value together, and if the hash matches then we save the result in another place in contract storage; an alternative approach is to use one single starting storage location and simply have four slots per hash instead of three. We return 1 is successful, and nothing for a failure. The third and fourth clauses are simply trivial data requests; the third is a balance check, and the fourth returns the contract’s current view of the price.
That’s all for the interface side of the contract; however, the one part that we still need to do is the part that actually aggregates the votes. We’ll break that up into parts. First, we have:
HASHES = 2^160 VALUES = 2^170 if block.number / 100 > contract.storage(0) / 100: # Sort all hashes N = contract.storage(1) o = array(N) i = 0 j = 0 while i < N: if contract.storage(VALUES + i): o(j) = contract.storage(VALUES + i) o(j + 1) = i j += 2 i += 1 values = call(contract.storage(3), o, j, j)
First, we use storage index 0 to store the last accessed epoch, and we check if the current epoch is higher than the last accessed epoch. If it is, then that signals the start of a new epoch, so we need to process all the votes and clear the contract for the next epoch. We start off by copying the values that have been submitted to an array (values that have not been submitted, ie. zeroes, are not put into this array). We keep two running counters, i and j; the counter i runs through all value slots, but the counter j counts only the value slots that have something inside them. Note that the array that we produce is of the form ( val1, index1, val2, index2 … ), where index1 etc are the indices of the associated values in the original values array in contract storage, thus for example, the following values would lead to the following array:
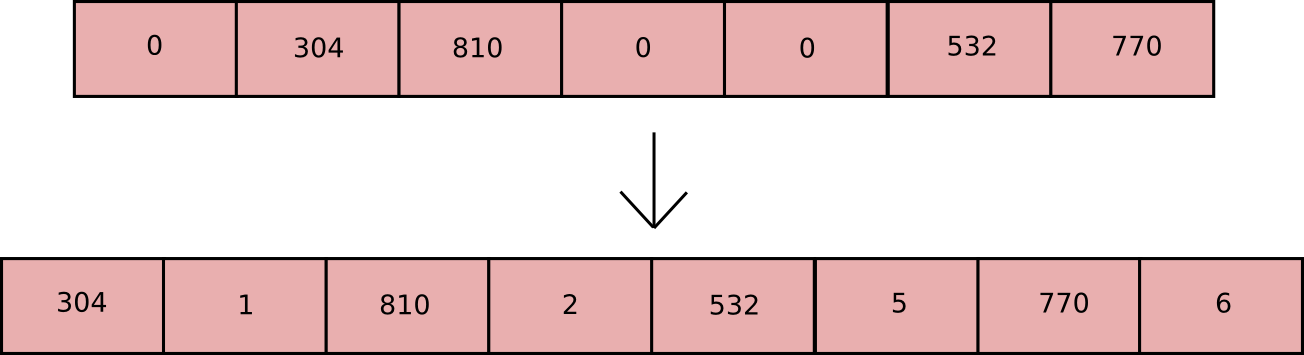
Then, we send that array through the quicksort contract, which sorts data pairs in the array. After the sort, we end up with:

Now, what we have is a sorted list of all the values that people have submitted, alongside pointers to where the associated metadata is stored in cold storage. The next part of the code will handle three things simultaneously. First, it will compute the total amount that has been deposited; this is useful in figuring out the median. Second, we will make two arrays to represent deposits and their associated addresses, and we will remove that data from the contract. Finally, we will 99.9% refund anyone who did not submit a value. Theoretically, we could make it a 70% refund or a 0% refund, but that might make the contract too risky for people to throw their life savings in (which is actually what we want in a proof-of-stake-weighted system; the more ether is thrown in by legitimate users the harder it is for an attacker to muster enough funds to launch an attack). here’s the code; feel free to understand each line yourself:
# Calculate total deposit, refund non-submitters and # cleanup deposits = array(j / 2) addresses = array(j / 2) i = 0 total_deposit = 0 while i < j / 2: base_index = HASHES + values(i * 2 + 1) * 3 contract.storage(base_index) = 0 deposits(i) = contract.storage(base_index + 1) contract.storage(base_index + 1) = 0 addresses(i) = contract.storage(base_index + 2) contract.storage(base_index + 2) = 0 if contract.storage(VALUES + values(i * 2 + 1)): total_deposit += deposits(i) else: send(addresses(i), deposits(i) * 999 / 1000) i += 1
Now, we come to the last part of the code, the part the computes the median and rewards people. According to the specification, we need to reward everyone between the 25th and 75th percentile, and take the median (ie. 50th percentile) as the truth. To actually do this, we needed to first sort the data; now that the data is sorted, however, it’s as simple as maintaining a running counter of “total deposited value of everything in the list up to this point”. If that value is between 25% and 75% of the total deposit, then we send a reward slightly greater than what they sent in, otherwise we send a slightly smaller reward. Here is the code:
inverse_profit_ratio = total_deposit / (contract.balance / 1000) + 1 # Reward everyone i = 0 running_deposit_sum = 0 halfway_passed = 0 while i < j / 2: new_deposit_sum = running_deposit_sum + deposits(i) if new_deposit_sum > total_deposit / 4 and running_deposit_sum < total_deposit * 3 / 4: send(addresses(i), deposits(i) + deposits(i) / inverse_profit_ratio * 3) else: send(addresses(i), deposits(i) - deposits(i) / inverse_profit_ratio) if not halfway_passed and new_deposit_sum > total_deposit / 2: contract.storage(2) = contract.storage(VALUES + i) halfway_passed = 1 contract.storage(VALUES + i) = 0 running_deposit_sum = new_deposit_sum i += 1 contract.storage(0) = block.number contract.storage(1) = 0
At the same time, you can see we also zero out the values in contract storage, and we update the epoch and reset the number of hashes to zero. The first value that we calculate, the “inverse profit ratio”, is basically the inverse of the “interest rate” you get on your deposit; if inverse_profit_ratio = 33333, and you submitted 1000000 wei, then you get 1000090 wei back if you are close to the median and 999970 if you are not (ie. your expected return is 1000030 wei). Note that although this amount is tiny, it happens per hundred blocks, so really it is quite large. And that’s all there is to it. If you want to test, then try running the following Python script:
import pyethereum t = pyethereum.tester s = t.state() s.mine(123) c = s.contract('schellingcoin.se') c2 = s.contract('schellinghelper.se') vals = ((125, 200), (126, 900), (127, 500), (128, 300), (133, 300), (135, 150), (135, 150)) s.send(t.k9, c, 10**15) print "Submitting hashes" for i, v in enumerate(vals): print s.send(t.keys(i), c, v(1), (1) + s.send(t.keys(i), c2, 0, (v(0), 12378971241241))) s.mine(50) print "Submitting vals" for i, v in enumerate(vals): if i != 5: print s.send(t.keys(i), c, 0, (2, i, v(0), 12378971241241)) else: print s.send(t.keys(i), c, 0, (2, i, 4)) print "Final check" s.mine(50) print s.send(t.k9, c, 0, (4))
Before running the script, be sure to fill the ‘schellinghelper.se’ file with return(sha3((msg.sender, msg.data(0), msg.data(1)), 3)); here, we’re just being lazy and using Serpent itself to help us put the hash together; in reality, this should definitely be done off-chain. If you do that, and run the script, the last value printed by the contract should return 127.
Note that this contract as it stands is not really scalable by itself; at 1000+ users, whoever supplies the first transaction at the start of each epoch would need to pay a very large amount of gas. The way to fix this economically is of course to reward the submitter of the transaction, and take a flat fee off every participant to pay for the reward. Also, however, the interest rate per epoch is tiny, so it may already not be worth it for users to participate unless they have a signigicant amount of cash, and the flat fee may make this problem even worse.
To allow people to participate with small amounts of ether, the simplest solution is to create a “stake pool” where people put their ether into a contract for the long term, and then the pool votes together, randomly selecting a participant weighted by stake to supply the value to vote for in each epoch. This would reduce the load from two transactions per user per epoch to three transactions per pool per epoch (eg. 1 pool = 1000 users) plus one transaction per user to deposit/withdraw. Note that, unlike Bitcoin mining pools, this stake pool is completely decentralized and blockchain-based, so it introduces at most very small centralization risks. However, this is an instructive example to show how a single contract or DAO may end up leading to an entire ecosystem of infrastructure working on the blockchain with contracts talking to each other; a specialized SchellingCoin blockchain would not be able to invent pooling mechanisms after the fact and integrate them so efficiently.
As far as applications go, the most immediate one is contracts for difference, and eventually a decentralized cryptographic US dollar; if you want to see an attempt at such a contract see here, although that code is almost certainly vulnerable to market manipulation attacks (buy a very large amount of USD inside the system, then buy USD on the market to move the price 0.5%, then sell the USD inside the system for a quick 0.3% profit). The core idea behind the decentralized crypto-dollar is simple: have a bank with two currencies, USD and ether (or rather, UScent and wei), with the ability to have a positive or negative quantity of dollars, and manipulate the interest rate on dollar deposits in order to keep the contract’s net dollar exposure always close to zero so that the contract does not have any net obligations in currencies that it does not have the ability to hold. A simpler approach would simply be to have an expanding-supply currency that adjusts its supply function to target the USD, but that is problematic because there is no protection if the value falls too much. These kinds of applications, however, will likely take quite a long time (in crypto terms; quite fast in traditional finance terms of course) to get built.


