BitVM 2: Opening the Arena

Last October, Zerosync’s Robin Linus dropped a little bombshell in the form of BitVM. One of the most long-standing criticisms of Bitcoin is that it is impossible to create an arbitrary program to control how money is spent or locked up. Bitcoin has very limited programmability in scripting languages ​​and the available primitives are extremely limited. You can verify signatures, add time locks to something, and manipulate data in a few simple ways, but that’s it.

Bitcoin UTXOs can be programmed to require signature verification, time lock verification, etc. However, it cannot be programmed to unlock based on arbitrary conditions. Robin’s insight into BitVM has been a single fundamental element in computing. could do At a physical/electrical level, it is implemented in the Bitcoin Script, a NAND gate, one of the fundamental building blocks of computing. Any possible computation can be composed of NAND gates.

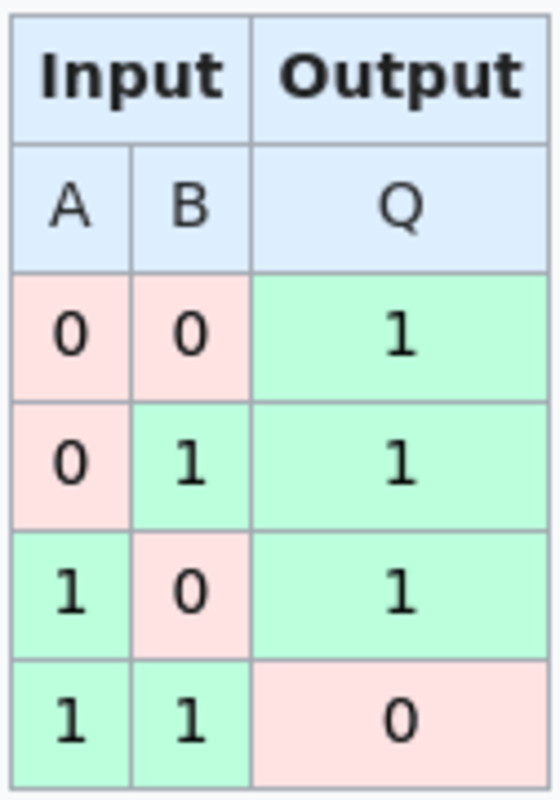
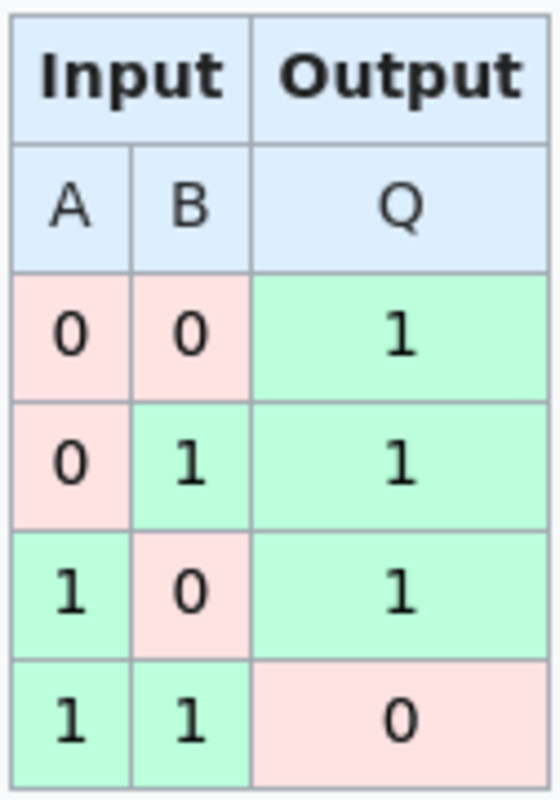
A neat trick with OP_BOOLAND and OP_NOT allows the script to actually check the NAND gate. OP_BOOLAND is an AND operation, as opposed to NAND. OP_NOT takes the binary 1 or 0 value and inverts it. This allows you to actually execute a single NAND operation directly from your script. Combined with hash locks, you can create a NAND gate script where each input and output field has two hash locks that can “unlock” the corresponding spend path. Each hash lock pushes a 1 or 0 onto the stack to perform a NAND operation. Each script also has a path that can be made public. both Convert your pre-image to a single bit value and you can claim your funds immediately. This is so that once someone decides what to put into the NAND gate, they can’t change their mind without losing money.

A huge amount of NAND gate scripts can all be compressed into a taproot tree, and once someone commits an off-chain bit value to feed into that computation, the adversary can challenge them to prove it at each individual step of the computation. It’s running correctly in the chain. Each “challenge” allows the offending party to prove that individual gates were calculated correctly. Otherwise, the other party may claim your funds after the time lock. This back and forth guarantees that if the calculations are disputed, the cheater will eventually be caught and the funds will be lost.

Limit

The main limitation of BitVM is that only those involved in BitVM contract creation can participate and their roles are very limited. There is a prover, who is the person who asserts how the computation occurred off-chain, and there is a verifier, who is the person who can challenge the computation and force it to be proven on-chain if the prover does not complete the computation off-chain, or attempts to do so. Lie about the results.

One of the reasons BitVM was designed was to establish a two-way peg to sidechains or other systems. This plan offers very powerful out-of-the-box functionality for its use case. That is, the ability to force one party or another to actually provide funds based on the correctness of an arbitrary calculation, i.e. validation of whether a pegout is valid according to the sidechain rules. . The problem is that only the person who holds the key to that BitVM UTXO can actually say, “Hey, you’re cheating!” Participate in the challenge protocol when someone is present. This ultimately makes the system still reliable.

Another limitation is that the challenge-response protocol can be very long. If someone realizes that they will lose money as a result of the computation and stops responding, the verifier will essentially have to guess where the individual NAND gates are in the computation where the prover should be, and reveal both pre-images. These are the bits that provide funds to validators. Until that particular gate is challenged on-chain, the prover can still correctly respond to the challenge and pull it. This can be time-consuming and inefficient.

Some improvements to this design have been made since the original proposal to allow multiple verifiers to exist in the system along with the prover to create a 1-of-n trust model where only one verifier is needed to challenge a dishonest prover. I lost. However, this requires instantiating multiple BitVM instances in parallel, increasing the inefficiency of the original two-party design.

BitVM 2

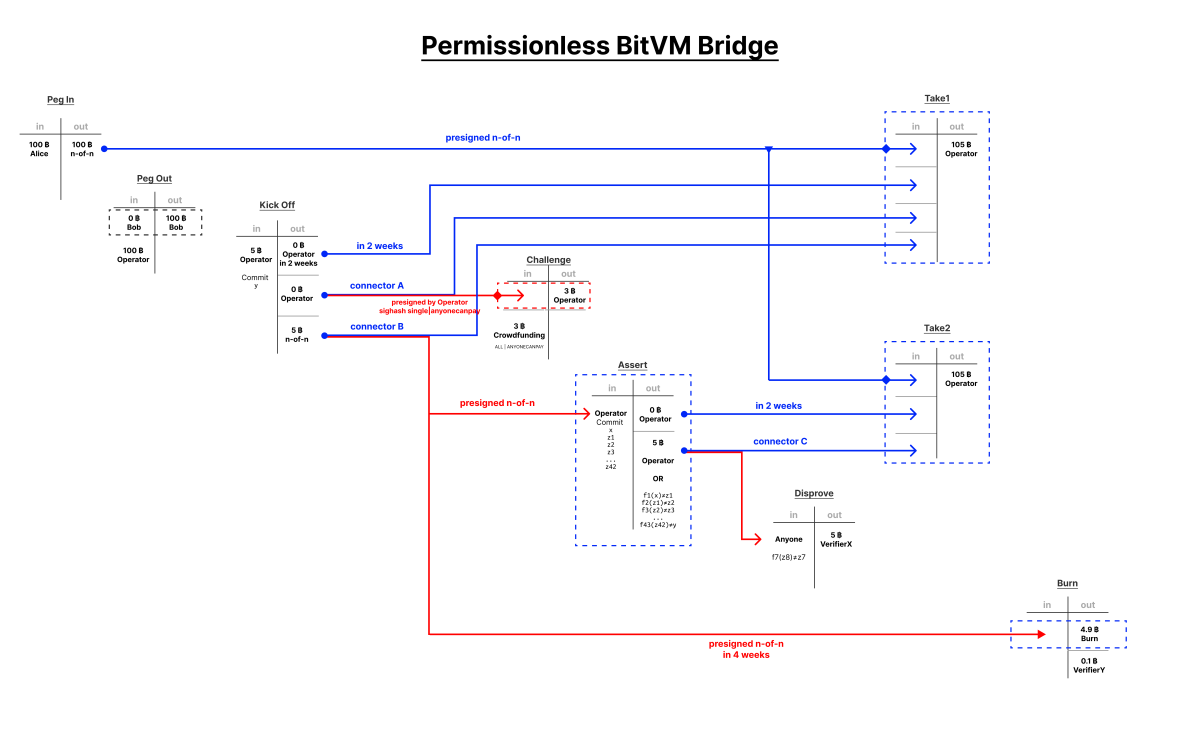
Robin recently proposed a design scheme for BitVM 2. This scheme explores several trade-offs compared to the original design for the benefit of mitigating two major drawbacks. BitVM 2 reduces the challenge/response protocol length to two rounds in an uncertain series of transactions, which could be dozens in the worst-case scenario. In addition to this, connector outputs allow you to: everyone Acts as a verifier. Someone does not need to be a participating member of the BitVM setup to challenge a dishonest prover.

The fundamental change here is to move away from directly using scripted NAND gates to directly implement the raw computation trace, and instead use them to implement a generic SNARK zero-knowledge proof verifier (one of the core primitives that Robin intended to implement using BitVM from the beginning). It’s about implementing it. ). Instead of putting raw input into a raw computation trace and executing it gate-by-gate in your own tapleaf script, the input to a BitVM 2 instance is just a zero-knowledge proof input combined with the computation’s assertion output.

In addition to abstracting the computational implementation using ZKP, the Tapleaf script is being massively expanded from a single NAND gate per leaf to a full sub-function of the ZKP verifier. Instead of a challenge-response protocol based on the verifier guessing which NAND gate the prover attempted to cheat on and the verifier selectively challenging a single gate, the verifier can prove that the output of an entire subfunction is invalid depending on its input.

Like BitVM 1, contracts are pre-negotiated using pre-signed transactions and branching scripts. Funds locked in BitVM are transferred as n-of-n multi-signatures that sign two possible executing transactions. One does not encounter a challenge and the other does. To begin the contract execution process, the prover initiates a kickoff transaction. This kickoff transaction commits to the output value ‘y’ that the computation claims to produce and has three outputs: the time lock output included in the challenge execution transaction, connector output A, and connector output B. Both are also used for challenge-free trading.

It is designed so that anyone can participate as a validator. Connector output A has a second pre-signed transaction, a challenge transaction, that can use it. This is a pre-signed transaction that pays the bond in Bitcoin to the prover, but the connector output A is not enough to fund it. Literally anyone can add their own input and use connector output A to fund a transaction. This invalidates the no-challenge withdrawal transaction for the prover (there exists one of the inputs that does not require a challenge).

This forces a challenging route. Connector output B can also be used using an assertion transaction, which is a pre-signed transaction for all subfunction outputs of the entire BitVM 2 contract. This requires a large transaction with a lot of data, but remember that the final output ‘y’ that the prover-generated computation asserts has already been committed in the initiating transaction. This will produce two outputs: One is timelocked output and the other is connector output C. Both of these outputs, in addition to being locked in the original funds, are both used in the prover’s second successful withdrawal transaction after the timelock.

Connector output C may also be used by anyone who can prove that the output of a subfunction of the BitVM 2 contract produces incorrect output. A very large transaction is required because the script required to prove an entire section of BitVM calculations is incorrect is massive, but in this single transaction the validator can claim coins from the connector output with a valid proof. This invalidates the prover’s second withdrawal transaction and effectively burns the coins. The only way to recover this at this point is with the prover. every All of the validators of the original n-of-n funds multisig work together to recover it. The connector output B of the kickoff transaction may be consumed after a much longer timeout than the no-challenge withdrawal, invalidating both the no-challenge and assertion transactions, thus burning the pegged coins.

This reduces what could have been an absurd chain of transactions in the original BitVM proposal for enforcing the correct contract outcome to a maximum of 4 transactions (albeit very large transactions), while at the same time creating a literal set of validators for BitVM 2 instances. Anyone holding Bitcoin who will fund the challenge transaction.

BitVM 2 could be an important innovation with respect to the wave of rollups and other layer 2s that seek to use BitVM as a two-way peg. Rollup operators (BitVM’s provers) can use their own funds to cover withdrawals from users locked in the system and reward themselves by withdrawing those funds from BitVM on a regular basis. any If users or stakeholders can provide evidence that the operator did not process all withdrawals correctly, they may be punished by burning their funds.

It is important to note that the security of a BitVM 2 instance is ultimately backstopped by n-of-n keyholders. Although non-participants can still challenge the prover as a validator. However, since the prover has efficient termination in the absence of a challenger and anyone can fund a challenge transaction to act as a verifier, n-of-n funded multisig could follow a setup and key deletion ritual similar to the Zcash launch. Improves security.

BitVM 2 will probably be a significant breakthrough in terms of improving the flexibility and trust model of the two-way peg using BitVM. Robin once again proved himself to be a true wizard.