Falcon Rig EA – Analysis and Forecast – December 3, 2023

introduction
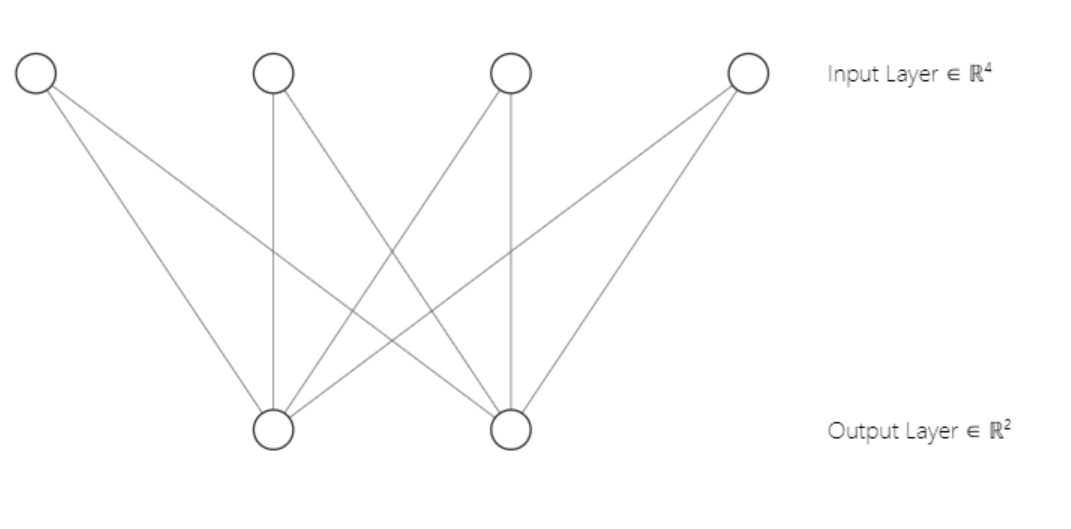
Kohonen Maps, Self-Organizing Maps (SOMs), or Self-Organizing Feature Maps (SOFM) are teacherless machine learning techniques that use low-dimensional (usually two-dimensional) spaces to represent multivariate data sets while preserving their topological structure. is used to generate . data. For example, you have a data set of p variables measured by n observations. This can be displayed as a cluster of observations with the same variable values. These clusters can then be represented as a two-dimensional map, where observations from closer clusters have more similar values than observations from distant clusters. This simplifies the visualization and analysis of multivariate data.
![]()
The Kohonen map was developed by Finnish mathematician Teuvo Kohonen in the 1980s..
General information
A Kohonen map consists of a grid of neurons connected to neighboring neurons. During training, input data is provided to the network and each neuron calculates its similarity to the input data. The neuron with the highest similarity is the winner, and its weights are adjusted to better match the input data.
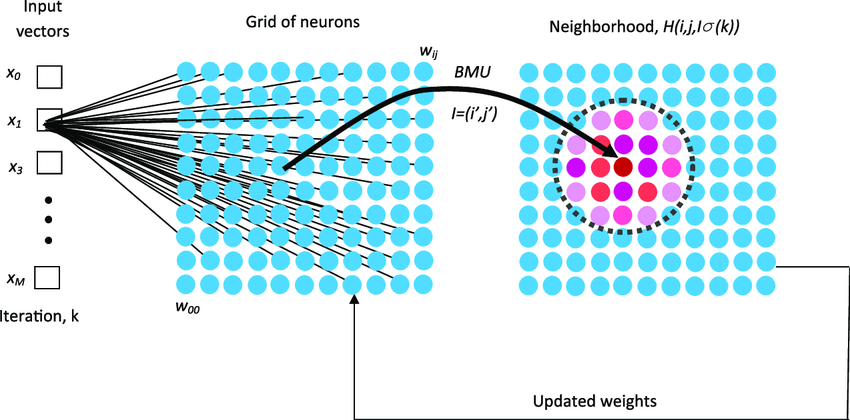
Over time, neighboring neurons also adjust their weights to become more similar to the winning neuron, resulting in the topological ordering of neurons in the map. This self-organizing process allows complex relationships between inputs to be expressed in a low-dimensional space through Kohonen maps. This feature is very useful for data visualization and clustering.
learning algorithm
The goal of the self-organizing map algorithm is to ensure that different parts of the network respond in the same way to specific input patterns. This is partly influenced by how visual, auditory, and other information is processed in certain parts of the human brain.
Let’s see how this algorithm applies to mathematical calculations and MQL5 code.
algorithm steps
Algorithm development consists of four main steps:
Step 1 is weight initialization. Any value can be used. Other parameters such as learning rate and number of clusters are also initialized in this step.
Unlike other types of artificial neural networks that learn with errors, such as backpropagation using gradient descent, self-organizing maps are a type of artificial neural network that uses competitive learning.
In competitive learning, neurons in a Kohonen map compete with each other to become the “winner.” This requires the neurons to be most similar to the input data.
During the training phase, each input data point is displayed on a Kohonen map. The similarity between the input data and each neuron’s weight vector is then calculated. The neuron whose vector is most similar to the input data is determined as the winner, or Best Matching Unit (BMU).
The BMU is selected based on the smallest Euclidean distance between the input data and the neuron’s weight vector. The winning neuron then updates its weight vector to make it more similar to the input data. The weight update formula used is the Kohonen learning rule, which moves the weight vectors of the winning neuron and its neighboring neurons closer to the input data.
Advantages of Kohonen Card
Kohonen maps have the following advantages:
Capture non-linear relationships between input data and output maps. This means it can handle complex patterns and data structures.
Find patterns in unlabeled data. That is, it can be used when labeled data is insufficient or difficult to obtain.
By reducing the dimensionality of the input data, the computational complexity of subsequent tasks such as regression and classification is reduced.
The topological relationship between input data and output map is maintained. Close neurons in the map correspond to similar regions of the input space, which can help with data exploration and visualization.
It is resistant to noise and outliers in the input data if the noise is too large.
conclusion
Kohonen maps, or self-organizing maps, are an innovative trading approach that can help traders navigate the markets. Using unsupervised learning, Kohonen Maps can identify patterns and structures in market data, allowing traders to make informed decisions. Kohonen maps can identify non-linear relationships in data and cluster data into appropriate groups. However, when working with them, you should be aware of potential drawbacks, such as sensitivity to initialization, lack of formal convergence criteria, etc. In general, Kohonen cards show excellent results in market transactions. I have been using Matrix and Kohonen cards in my business. New EA Falcon Rig EA available to try on deal now.



