The 1.x Files: GHOST in the Stack Machine

Ethereum can be simple enough to understand from a bird’s-eye view: Decentralized applications powered by the same sort of crypto-economic guarantees that underpin Bitcoin. But once you’ve zoomed in to, say, a street-level view, things get complicated rapidly.
Even assuming one has a strong grasp on proof-of-work, it’s not immediately clear how that translates to a blockchain doing more than keeping track of everyone’s unspent transaction outputs. Bitcoin uses computational work to decentralize money. Ethereum uses computational work to decentralize abstract computation. Wut? That abstraction is called the Ethereum Virtual Machine, and it’s the centerpiece of the Ethereum protocol, because “inside” the EVM is the special domain of smart contracts, and it’s the smart contracts that are ultimately to blame for all those ridiculous #defi tweets.
Upgrading the EVM is one of the major milestones of the Stateless Ethereum Tech Tree, and before we can dig in to the interesting work there, I think it’s prudent to first tackle the obvious question: “WTF is the EVM?”. In the first of this two-part series, we’ll get back to basics and try to understand the EVM from the ground up, so that later we can really engage with current discussion about things like Code Merklization and UNGAS— even stuff from the exciting world of Eth2 like Execution Environments!
WTF is the EVM?
When first year Algebra students get taught about that familiar function f(x), an analogy of “the function machine” is often used. The concept of deterministic input/output, it seems, is a lot easier for kids to think about as a literal physical machine chugging along. I like this analogy because it cuts both ways: The EVM, which in a way actually is a literal machine chugging along, can be thought about as a function which accepts as inputs some state and outputs a new one based on some arbitrary set of rules.
Setting aside the specifics of those rules for now, say that the only valid state transitions are the ones that come from valid transactions (that follow the rules). The abstract machine that will determine a new state (S’) given an old valid state (S) and a new set of valid transactions (T) is the Ethereum state transition function:
Y(S, T)= S’
The first thing that’s very important to understand about this function is that, as an abstraction, it’s sort of a mathematical placeholder: arguably not a real thing, and definitely not the EVM. The Ethereum state transition function is written all fancy in Greek in the yellow paper because thinking about the EVM as a black box function really helps with imagining the whole blockchain system (of which the EVM is just one part). The two-way connection between functions and machines is determinism: Given any valid input, both should produce one and only one output.
But the EVM, as I said before, is in some sense a literal machine chugging along out there in the world. The EVM’s physical instantiation can’t be described in the same way that one might point to a cloud or an ocean wave, but it does exist inside thousands of connected computers running Ethereum clients. And at any given time, there is one and only one canonical Ethereum state, and that’s what we care about. All of the other components inside an Ethereum client are there just to keep consensus over which state is the right one.
The term ‘canonical’ is used because ‘valid’ isn’t quite appropriate; a state transition computed correctly is ‘valid’, but it still might not end up “on chain” as part of the canon. Deciding which states are canonical and which states are not is the sole responsibility of miners doing proof-of-work on the chain. Anyone using Ethereum mainnet has, either literally or just figuratively, “bought in” to one particular state history, namely the one with the most computational work put behind it, as determined by Ethereum’s Greedy Heaviest Observed Subtree (GHOST) protocol. Along with each new block on the network comes a new set of transactions, a state transition, and a freshly determined output state ready to be passed forward into the next canonical block, determined by miners. And so on and so forth; that is how the Ethereum blockchain do.
We’ve so far ‘black-boxed’ the EVM as the state transition function (machine) that takes previous valid blocks and a handful of fresh transactions (as input), does some computation on it, and spits out a new valid state (as output). The other pieces of the Ethereum protocol (such as miners choosing canonical blocks) are necessary context, but now it’s time for some inside-the-box thinking. What about those specific rules we set aside earlier? How does the EVM compute a new state? How can a single machine compute everything from simple balance transfers to elliptic curve algebra?
The Steampunk Stack Machine
The best I can do to introduce the notion of a stack machine is this cartoon image of Babbage’s Analytical Engine (credit: Sydney Padua), which was designed in 1837 but never built:

With most people carrying around fantastically powerful electric computers in their pockets these days, it’s easy to forget that computers don’t necessarily need to be electronic, nor all that powerful. Babbage’s Analytical Engine is a very (hypothetically) real example of a Turing-complete (!) computer that if it had been built, would’ve run on steam and punch cards. The EVM is in important ways much closer kin to the Analytical Engine of two centuries ago than to the CPU inside the device you’re using to read this article.
The EVM is a stack machine, and although in reality it’s a virtualized machine running inside many Ethereum clients simultaneously, I find helpful to imagine the EVM as a real, more advanced (but of course still steam-powered) version of the Analytical Engine. This metaphor might seem a little far-fetched, but I implore you to stick with it for a little bit because it’s quite illustrative when we get to the subject of gas and a shared execution environment.
The steampunk EVM would be a mechanical computer that functions by manipulating physical punch cards. Each card would have 256 places for hole punches, and therefore each card could represent any number between 0 and 2^256. To perform a calculation, one could imagine this computer, through some fancy system of compressed air, putting the cards representing numbers and operations into a stack, and following a simple principle of “first in, last out”, one-by-one it would PUSH new cards to the top of the stack, or POP cards from the top of the stack to read them for next steps. These might be new numbers to calculate with, or arithmetic operations like ADD or MULTIPLY, but they could also be special instructions such as to STORE a card or set of cards for later. Because the cards are simple binary, the operations also have to be ‘encoded’ into a binary number; so we call them operational codes, or just opcodes for short.
If the stack machine were calculating 4 * 5 + 12, it would go about it like so:
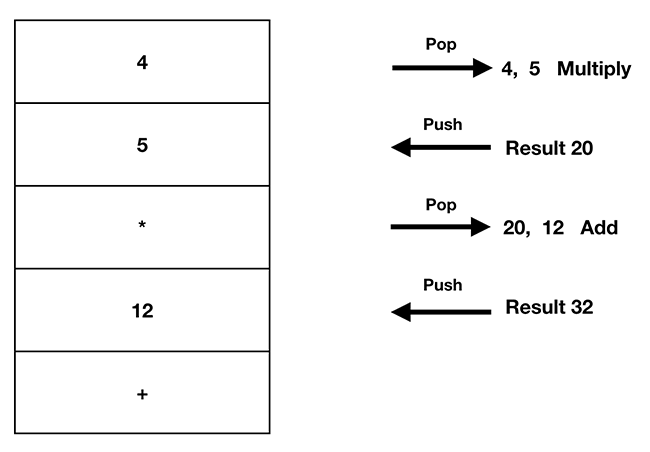
_POP value 4 from the stack, keep it in memory. POP the value 5 off the stack, keep it in memory. POP the value _ from the stack; send everything in memory to the multiplication module; PUSH the returned result (20) the stack. POP the value 20 from the stack; keep it in memory. POP the value 12 from the stack; keep it in memory. POP the value + from the stack; send everything in memory to the addition module; PUSH the returned result (32) the stack. (Source: The EVM Runtime Environment)
We can imagine opcodes like ADD or MULTIPLY as special modules built into the machine, near enough to the stack so as to be accessible quickly. When the computer must multiply 4 and 5, it would send both cards to the “multiplication engine”, which might click and hiss before spitting back out the number 20 punched into a new card to PUSH back to the top of the stack.
The “real” EVM has many different opcodes for doing various things. A certain minimum-viable set of these opcodes are needed to do generalized computation, and the EVM has all of them (along with some special ones for crypto, e.g. the SHA-3 hash function). For better or worse, the idea that the EVM is (or is not) Turing-complete has long been under discussion— it’s this stack-based architecture which has the property of Turing-completeness: The EVM’s rules of execution can in principle, given a long enough time and big enough memory, run any conceivable computer program so long as it’s compiled down to the correct 256-bit words and executed in the stack.
Compiling a program in our alternate universe would entail the creation of a booklet of punch cards containing the appropriate data and opcodes. This is literally (er, figurative-literally, whatever) the process going on under the hood when you write a smart contract in a high-level language like Solidity and compile it to bytecode. You can get a pretty good sense of how a programming language gets converted into machine code by reading this humerously annotated output of a Solidity compiler.
So far, the state has not been mentioned, but recall that we set out to understand the rules by which a state transition can be calculated. Now we can summarize it a bit more clearly: The EVM is the physical instantiation (read: instance) of the state transition function. A valid state in Ethereum is one that was calculated by the EVM, and the canonical state is the valid state with the most computational work done on it (as determined by the GHOST protocol).
(Ideal) Gas
We might imagine Babbage completing the fictitious Ethereum Stack Engine and thereafter announcing that all mathematical tabulations and solutions for impossibly difficult problems were now within reach. He’d invite mathematicians and engineers to package up their problems as ‘transactions’ and deliver them to be compiled by Lady Lovelace into punch cards to run through the world computer. (Incidentally, Lovelace was the first person to ever write a computer program, making her the original compiler). Since the machine is meant to be an implementation of the EVM and part of a larger Ethereum steampunk universe, we’d have to imagine the state as being some sort of massive Merkleized library catalog which would be updated once per day according to a pre-selected set and order of transactions chosen as ‘canonical’, and committed to archive.
The trouble with this vision is that a real, mechanical EVM would be extraordinarily expensive to run. The turning of gears, winding of springs, and pumping of various pneumatic chambers collating punch cards would use tonnes of coal every day. Who would bear the expense of running the engine constantly? Say that five mathematicians wanted to run their programs on a particular day, but there was only time enough for three. How would these and related problems of resource management be solved? The solution that Ethereum employs seems, paradoxically, a lot more intuitive when we think about a large and inefficient mechanical computer: Charge money for computation and memory storage!
Imagining the the operations of the stack machine to be powered by compressed air, one could measure the exact amount of gas needed to perform an ADD operation, and compare it to the (much larger) amount of gas needed for SHA3. The table of gas costs for each opcode could be made publicly available, and anyone submitting a program required to provide at least enough money for their computation and storage space according to the cost of gas (which might be related to the price of coal or the demand for computation). The final stroke of genius is to make the machine state itself a ledger for accounts and balances, allowing a user to include payment for their computation inside the transaction itself.
As you might know, gas in an Ethereum transaction accounts for computation and memory costs of the EVM. Gas costs for a transaction must be paid for in ETH, and cannot be recovered once the execution takes place, whether the operation succeeds or not. If a contract call runs out of gas at any point during an operation, it throws an out-of-gas error.
The gas mechanic cleverly does two jobs: Gas efficiently allocates the common-pool computational resources of the EVM according to demand, and provides reasonable protection against infinitely looping programs (a problem that arises from Turing-completeness).
In the next installment of “The 1.X Files”
I hope this fanciful mechanical explanation of a stack machine has been helpful. If you enjoyed thinking about the steampunk EVM as much as I have, and you like historically plausible alt-reality comic books, do investigate “The Thrilling Adventures of Babbage and Lovelace” linked earlier; you won’t be disappointed.
Getting a handle on something so abstract isn’t easy, but there are topics in the Stateless Tech Tree that will be much easier to approach with a relatively complete (even if it’s a bit cartoonish) mental image of an EVM implementation.
One such topic is the introduction of Code Merkleization to the EVM, which would greatly reduce the size of witnesses by breaking up compiled contract code into smaller chunks. Next time we’ll be able to dig in to these immediately.
As always, if you have any questions, comments, requests for new topics or steampunk Ethereum fanfictions, please @gichiba or @JHancock on twitter.



