P + Epsilon Attack

Special thanks to Andrew Miller for coming up with this attack, and Zack Hess, Vlad Zamfir, and Paul Sztorc for discussion and response.
One of the most interesting surprises in cryptoeconomics in recent weeks is Schelling Coin It was conceived by Andrew Miller earlier this month. SchellingCoin and similar systems (including more advanced ones) have always been understood. Truth Coin consensus), which relies on new and hitherto untested cryptoeconomic security assumptions. This means that we can safely rely on people acting honestly in a simultaneous consensus game because they trust everyone else to do so. The issues raised so far are: It has to do with relatively minor issues, such as the attacker’s ability to exert a small but growing influence on output over time by applying sustained pressure. On the other hand, this attack illustrates a much more fundamental problem.
The scenario is described as follows: Suppose we have a simple Schelling game in which users vote on whether a particular fact is true (1) or false (0). In our example, say it’s actually false. Each user can vote 1 or 0. If users vote with a majority, they receive a reward of P. Otherwise you get 0. So the payoff matrix is:
| You voted 0 | you voted 1 | |
| Other 0 votes | blood | 0 |
| Others voted 1 | 0 | blood |
The theory is that if everyone expects everyone else to vote truthfully, then their incentive is to vote truthfully to comply with the majority, which is why they can expect others to vote truthfully in the first place. Self-reinforcing Nash equilibrium.
Now for the attack. It is said that the attacker has trustworthyly promised Assume: = P + ε (if majority vote is 0), X = 0 (if majority vote is 1). Now the payoff matrix is:
| You voted 0 | you voted 1 | |
| Other 0 votes | blood | P + e |
| Others voted 1 | 0 | blood |
So the prevailing strategy is for everyone to vote No. 1, regardless of what they think the majority will do. So, assuming the system is not dominated by altruists, the majority votes 1, so the attacker doesn’t have to pay anything at all. The attack succeeded in taking over the mechanism without cost. Note that this differs from Nicholas Houy’s argument. 51% attack without the cost of proof-of-stake (A claim technically scalable with ASIC-based proof-of-work) Epistemological Argument Required. Even if everyone is confident that the attacker will fail, there is still an incentive to vote in support of the attacker. This is because the attacker assumes the risk of failure himself.
Schelling Plan Recall
There are several steps you can take to rescue the Schelling mechanism. One approach is to use Round N + 1 to determine who should receive compensation during Round N, instead of Round N in the Schelling agreement itself, which relies on “majority rule” principles to determine who should receive compensation. People who voted correctly in N rounds (on the actual facts of the matter and who should be rewarded in N-1 rounds) should be rewarded. In theory, this would require the attacker to perform a cost-free attack to compromise not just one round, but all future rounds, creating the required capital deposit that the attacker must make indefinite.
However, there are two flaws with this approach. First, the mechanism is fragile. If the attacker can compromise some rounds in the distant future by paying everyone P+ε, regardless of who actually wins, then the expectation of a compromised round creates an incentive to cooperate with the attacker. Backpropagates to all previous rounds. So damaging one round is expensive, but damaging thousands of rounds is not so costly.
Second, because discount, the deposit required to overcome this scheme does not have to be infinite. It just has to be very large (i.e. inversely proportional to prevailing interest rates). But if what we want is to increase the minimum level of bribery, there is a much simpler and better strategy for doing so. Pioneered by Paul Storcz: Require participants to make large deposits, and build a mechanism where the more disputes there are, the more funds are at stake. At the threshold of just over 50% voting in favor of one outcome and 50% voting in favor of the other, the entire deposit was taken away from minority voters. This way the attack still works, but the bribe must now be greater than the deposit (roughly equal to the payout divided by the discount rate, giving the same performance in infinite round games) rather than the payout for each round. So to overcome these mechanisms you would need to be able to prove that a 51% attack could be performed, and perhaps it would be comfortable to assume that attackers of that scale do not exist.
Another approach is to rely on counter-coordination. Essentially, we somehow coordinate, perhaps through a trustworthy promise, the vote of A (if A is true) with probability 0.6 and the vote of B with probability 0.4. In theory, this allows users to claim (probably) a portion of the mechanism’s rewards. At the same time, the attacker’s bribe. This appears to work particularly well in games that are structured to have a constant total reward, rather than paying a constant reward to each majority voter, and individual rewards must be adjusted to achieve this goal. In this situation, from the perspective of group rationality, the group would benefit the most if 49% of its members vote for B to demand the attacker’s reward and 51% of A votes to ensure that the attacker’s reward is paid. It actually exists. .
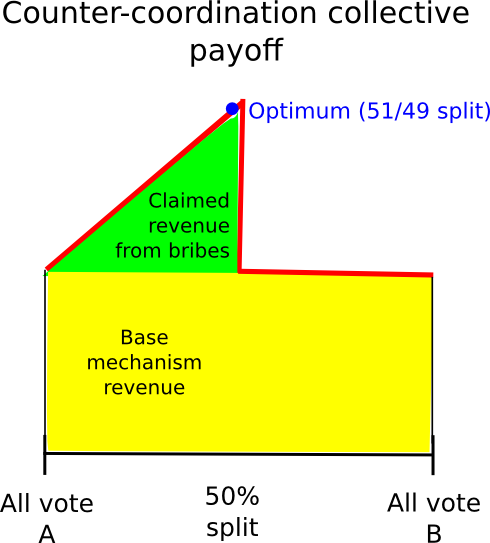
However, this approach itself has a flaw: if the attacker’s bribe is high enough, they can betray there too. The fundamental problem is that, given a stochastic mixed strategy between A and B, the return on each always varies (approximately) linearly with the stochastic parameters. Therefore, if it is more rational for an individual to vote for B than A, it would be more rational to vote for B with probability 0.51 than to vote for B with probability 0.49, and voting for B with probability 1 would also work. no see. Better.
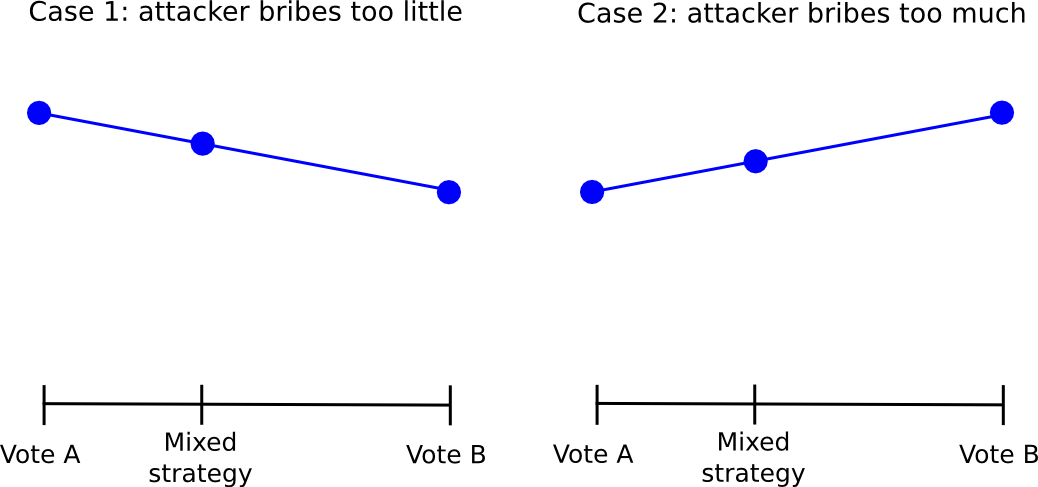
Therefore, by simply always voting for 1, everyone gets out of the “49% for 1” strategy, so 1 wins and the attacker gets a cost-free takeover. The fact that such complex schemes exist and are so close to “appearing to work” suggests that perhaps in the near future we will see complex counter-coordination schemes that actually work. But we must be prepared in case such a plan is not developed.
Additional results
Considering the number of cryptocurrency economic mechanisms that SchellingCoin enables and the importance of these schemes in almost all purely “trustless” attempts to establish any kind of connection between the crypto world and the real world, this attack poses a potentially serious threat. I raise it. – As we will see later, Schelling’s plan as a category is ultimately partially salvageable. But what’s more interesting is that while at first glance it doesn’t look at all similar to SchellingCoin, it is actually a much larger class of mechanism with very similar strengths and weaknesses.
In particular, let’s take a very specific example: proof-of-work. Proof-of-Work is actually a multiple equilibrium game in much the same way as a Schelling scheme. If you have two forks A and B, if you mine on the fork and end up winning, you get 25 BTC, and if you mine on the fork you end up losing, you get nothing.
| You’re mine from A | You’re mine in B | |
| Others mine A. | 25 | 0 |
| Others mine B | 0 | 25 |
Now assume that an attacker launches a double-spend attack against multiple parties simultaneously (this requirement ensures that no single party has a very strong incentive to oppose the attacker, and instead opposition becomes a public good. Alternatively, double-spend is purely An attacker attempts to crash the price by selling with 10x leverage, calling the “main” chain A and the attacker’s new double-spending fork B. Basically, everyone expects A to win. However, the attacker expects B to eventually win. In case of a loss, we promise to pay 25.01 BTC to everyone who mines B. So the payoff matrix is:
| You’re mine from A | You’re mine in B | |
| Others mine A. | 25 | 25.01 |
| Others mine B | 0 | 25 |
Therefore, since mining for B is the dominant strategy regardless of an individual’s epistemic beliefs, everyone is mining for B, so the attacker wins and pays nothing. In particular, since proof-of-work has no deposit, the level of bribe required is only proportional to the mining reward multiplied by the fork length, rather than the capital cost of 51% of the total mining rig. So from a cryptoeconomic security perspective, in a sense, we can say that proof-of-work has virtually no cryptoeconomic security margin at all. This article by Andrew Poelstraplease link your answer to this here.) If you are really uncomfortable, weak subjectivity If pure proof-of-stake is the requirement, augmenting proof-of-work with hybrid proof-of-stake by adding a deposit and double voting penalty to mining may be the right solution.
Of course, in reality, despite these flaws, proof-of-work has survived, and may indeed continue to survive for a long time. It may be the case that the altruism is high enough that the attacker is not 100% sure that he will actually succeed. However, naive proof-of-stake also works well if you can rely on altruism. So even though the Schelling plan may not be perfect in theory, it may end up working in practice.
In the next part of this post, we will discuss the concept of “subjective” mechanisms and how these mechanisms can be used to theoretically solve some of these problems.



